您现在的位置是: 首页 > 考试作文 考试作文
五年级上册数学知识点整理归纳
zmhk 2024-05-18 人已围观
简介五年级上册数学知识点整理归纳 大家好,今天我将为大家讲解五年级上册数学知识点整理归纳的问题。为了让大家更好地理解这个问题,我将相关资料进行了整理,现在就让我们一起来看看吧。1.人教版小学数学五年级上册知识点有哪些
大家好,今天我将为大家讲解五年级上册数学知识点整理归纳的问题。为了让大家更好地理解这个问题,我将相关资料进行了整理,现在就让我们一起来看看吧。
1.人教版小学数学五年级上册知识点有哪些
2.五年级上册数学知识点三篇1-3单元
3.北师大版小学五年级数学上册知识点
人教版小学数学五年级上册知识点有哪些
小学五年级数学上册复习教学知识点归纳总结
第一单元小数乘法
1、小数乘整数(P2、3):意义——求几个相同加数的和的简便运算.
如:1.5×3表示1.5的3倍是多少或3个1.5的和的简便运算.
计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点.
2、小数乘小数(P4、5):意义——就是求这个数的几分之几是多少.
如:1.5×0.8就是求1.5的十分之八是多少.
1.5×1.8就是求1.5的1.8倍是多少.
计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点.
注意:计算结果中,小数部分末尾的0要去掉,把小数化简;小数部分位数不够时,要用0占位.
3、规律(1)(P9):一个数(0除外)乘大于1的数,积比原来的数大;
一个数(0除外)乘小于1的数,积比原来的数小.
4、求近似数的方法一般有三种:(P10)
⑴四舍五入法;⑵进一法;⑶去尾法
5、计算钱数,保留两位小数,表示计算到分.保留一位小数,表示计算到角.
6、(P11)小数四则运算顺序跟整数是一样的.
7、运算定律和性质:
加法:加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c)
减法:减法性质:a-b-c=a-(b+c) a-(b-c)=a-b+c
乘法:乘法交换律:a×b=b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法分配律:(a+b)×c=a×c+b×c(a-b)×c=a×c-b×c
除法:除法性质:a÷b÷c=a÷(b×c)
第二单元小数除法
8、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算.
如:0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3,求另一个因数的运算.
9、小数除以整数的计算方法(P16):小数除以整数,按整数除法的方法去除.,商的小数点要和被除数的小数点对齐.整数部分不够除,商0,点上小数点.如果有余数,要添0再除.
10、(P21)除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算.
注意:如果被除数的位数不够,在被除数的末尾用0补足.
11、(P23)在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数.
12、(P24、25)除法中的变化规律:①商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变.②除数不变,被除数扩大,商随着扩大.③被除数不变,除数缩小,商扩大.
13、(P28)循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数.
循环节:一个循环小数的小数部分,依次不断重复出现的数字.如6.3232……的循环节是32.
14、小数部分的位数是有限的小数,叫做有限小数.小数部分的位数是无限的小数,叫做无限小数.
第三单元观察物体
15、从不同的角度观察物体,看到的形状可能是不同的;观察长方体或正方体时,从固定位置最多能看到三个面.
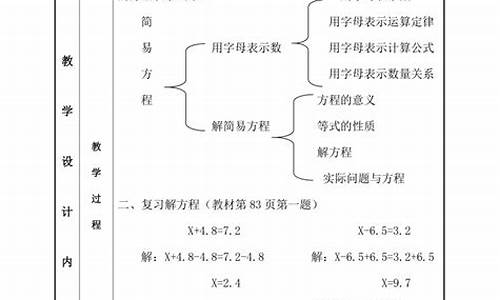
第四单元简易方程
16、(P45)在含有字母的式子里,字母中间的乘号可以记作“ ”,也可以省略不写.
加号、减号除号以及数与数之间的乘号不能省略.
17、a×a可以写作a a或a ,a 读作a的平方. 2a表示a+a
18、方程:含有未知数的等式称为方程.
使方程左右两边相等的未知数的值,叫做方程的解.
求方程的解的过程叫做解方程.
19、解方程原理:天平平衡.
等式左右两边同时加、减、乘、除相同的数(0除外),等式依然成立.
20、10个数量关系式:加法:和=加数+加数 一个加数=和-两一个加数
减法:差=被减数-减数 被减数=差+减数 减数=被减数-差
乘法:积=因数×因数 一个因数=积÷另一个因数
除法:商=被除数÷除数 被除数=商×除数 除数=被除数÷商
21、所有的方程都是等式,但等式不一定都是等式.
22、方程的检验过程:方程左边=……
23、方程的解是一个数;
解方程式一个计算过程.=方程右边
所以,X=…是方程的解.
第五单元多边形的面积
23、公式:长方形:周长=(长+宽)×2——长=周长÷2-宽;宽=周长÷2-长 字母公式:C=(a+b)×2
面积=长×宽
五年级上册数学知识点三篇1-3单元
1. 五年级数学小知识
五年级数学小知识 1. 小学五年级数学知识点
小学五年级数学上册期末复习知识点归纳第一单元小数乘法1、小数乘整数(P2、3):意义——求几个相同加数的和的简便运算。
如:1.5*3表示1.5的3倍是多少或3个1.5的和的简便运算。计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
2、小数乘小数(P4、5):意义——就是求这个数的几分之几是多少。如:1.5*0.8就是求1.5的十分之八是多少。
1.5*1.8就是求1.5的1.8倍是多少。计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
注意:计算结果中,小数部分末尾的0要去掉,把小数化简;小数部分位数不够时,要用0占位。3、规律(1)(P9):一个数(0除外)乘大于1的数,积比原来的数大; 一个数(0除外)乘小于1的数,积比原来的数小。
4、求近似数的方法一般有三种:(P10)⑴四舍五入法;⑵进一法;⑶去尾法5、计算钱数,保留两位小数,表示计算到分。保留一位小数,表示计算到角。
6、(P11)小数四则运算顺序跟整数是一样的。7、运算定律和性质:加法:加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c)减法:减法性质:a-b-c=a-(b+c) a-(b-c)=a-b+c乘法:乘法交换律:a*b=b*a乘法结合律:(a*b)*c=a*(b*c)乘法分配律:(a+b)*c=a*c+b*c(a-b)*c=a*c-b*c除法:除法性质:a÷b÷c=a÷(b*c)第二单元小数除法8、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3,求另一个因数的运算。9、小数除以整数的计算方法(P16):小数除以整数,按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。整数部分不够除,商0,点上小数点。
如果有余数,要添0再除。10、(P21)除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用0补足。11、(P23)在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。
12、(P24、25)除法中的变化规律:①商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。②除数不变,被除数扩大,商随着扩大。
③被除数不变,除数缩小,商扩大。13、(P28)循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
循环节:一个循环小数的小数部分,依次不断重复出现的数字。如6.3232……的循环节是32.14、小数部分的位数是有限的小数,叫做有限小数。
小数部分的位数是无限的小数,叫做无限小数。第三单元观察物体15、从不同的角度观察物体,看到的形状可能是不同的;观察长方体或正方体时,从固定位置最多能看到三个面。
第四单元简易方程16、(P45)在含有字母的式子里,字母中间的乘号可以记作“?”,也可以省略不写。加号、减号除号以及数与数之间的乘号不能省略。
17、a*a可以写作a?a或a ,a 读作a的平方。 2a表示a+a18、方程:含有未知数的等式称为方程。
使方程左右两边相等的未知数的值,叫做方程的解。求方程的解的过程叫做解方程。
19、解方程原理:天平平衡。 等式左右两边同时加、减、乘、除相同的数(0除外),等式依然成立。
20、10个数量关系式:加法:和=加数+加数 一个加数=和-两一个加数 减法:差=被减数-减数 被减数=差+减数 减数=被减数-差 乘法:积=因数*因数 一个因数=积÷另一个因数 除法:商=被除数÷除数 被除数=商*除数 除数=被除数÷商21、所有的方程都是等式,但等式不一定都是等式。22、方程的检验过程:方程左边=…… 23、方程的解是一个数; =…… 解方程式一个计算过程。
=方程右边 所以,X=…是方程的解。第五单元多边形的面积23、公式:长方形:周长=(长+宽)*2——长=周长÷2-宽;宽=周长÷2-长 字母公式:C=(a+b)*2 面积=长*宽 字母公式:S=ab 正方形:周长=边长*4 字母公式:C=4a 面积=边长*边长 字母公式:S=a平行四边形的面积=底*高 字母公式: S=ah三角形的面积=底*高÷2 ——底=面积*2÷高;高=面积*2÷底 字母公式: S=ah÷2梯形的面积=(上底+下底)*高÷2 字母公式: S=(a+b)h÷2——上底=面积*2÷高-下底,下底=面积*2÷高-上底;高=面积*2÷(上底+下底)24、平行四边形面积公式推导:剪拼、平移 25、三角形面积公式推导:旋转 平行四边形可以转化成一个长方形; 两个完全一样的三角形可以拼成一个平行四边形, 长方形的长相当于平行四边形的底; 平行四边形的底相当于三角形的底; 长方形的宽相当于平行四边形的高; 平行四边形的高相当于三角形的高; 长方形的面积等于平行四边形的面积, 平行四边形的面积等于三角形面积的2倍,因为长方形面积=长*宽,所以平行四边形面积=底*高。
因为平行四边形面积=底*高,所以三角形面积=底*高÷226、梯形面积公式推导:旋转 27、三角形、梯形的第二种推导。
2. 5年级的数学小知识
一 数学笑话1.有一次,妈妈很耐心地启发丫丫做算术题:“丫丫,你已经学会做减法了,对吗?来,我们来看看,4减2等于几?” “等于2,妈妈。”
“太对了,乖孩子。那么,5减5呢?” “5减5,减5。
.”丫丫嘟哝着,“我不会,妈妈。”
“孩子,你不可能不会!想想,比如说你口袋里装着5枚硬币,可是,突然,5枚硬币都掉了。你说,口袋里还有什么?” 丫丫忽闪着两只大眼睛,说道:“掉了?那,那我的口袋里还有一个洞呀!” 2.“考算术,我总得100。”
“那是你学得好。” “可我上课从来不听讲。”
“那是你聪明,而且放学回家知道用功。” “聪明吗?倒有点,可放学后,我是一个与足球打交道的人。”
“那么你考试时,一定是靠作弊。” “不能这么说,我既没打小条抄书,又没偷看人家的,怎么算是作弊。”
“那你怎么搞的?” “我用脚踢前面的书呆子吉姆的椅子。” “不会就不会,怎么能这么淘气。”
“我踢第一脚,他用手朝后伸出五个指头。” “这是什么意思?” “第一题2+3的答案。”
“噢……要是问第十题5*8的答案呢?” “那是在我踢完第十脚以后,他先伸出四个指头,然后马上握紧拳头,于是我就知道40这个答案了。” 3.老师发表成绩:"小华三十分、小明二十分……” 小猪: 我考0 分耶! 小狗: 怎么办, 我也是耶…… 小猪: 我们两个考同分, 老师会不会以为我们作弊啊? 二 数学故事 相传有一天,诸葛亮把将士们召集在一起,说:“你们中间不论谁,从1~1024中任意选出一个整数,记在心里,我提十个问题,只要求回答‘是’或‘不是’。
十个问题全答完以后,我就会‘算’出你心里记的那个数。”诸葛亮刚说完,一个谋士站起来说,他已经选好了一个数。
诸葛亮问道:“你选的数大于512?”谋士答:“不是。”诸葛亮又接连向这谋士提了九个问题,谋士都一一作了回答。
诸葛亮最后说:“你记的那个数是1。”谋士听了极为惊奇,因为这个数果真是他选的数。
你知道诸葛亮是怎样妙算的吗? 其实方法很简单,就是把1024一半一半的取,取到第十次时,就是“1”。根据这个道理,连续提十个问题,就能找到所需的数。
三.数学名言1.、王菊珍的百分数 我国科学家王菊珍对待实验失败有句格言,叫做“干下去还有50%成功的希望,不干便是100%的失败。” 2、托尔斯泰的分数 俄国大文豪托尔斯泰在谈到人的评价时,把人比作一个分数。
他说:“一个人就好像一个分数,他的实际才能好比分子,而他对自己的估价好比分母。分母越大,则分数的值就越小。”
1、数学的本质在於它的自由. 康扥尔(Cantor) 2、在数学的领域中, 提出问题的艺术比解答问题的艺术更为重要. 康扥尔(Cantor) 3、没有任何问题可以向无穷那样深深的触动人的情感, 很少有别的观念能像无穷那样激励理智产生富有成果的思想, 然而也没有任何其他的概念能向无穷那样需要加以阐明. 希尔伯特(Hilbert) 4、数学是无穷的科学. 赫尔曼外尔 5、问题是数学的心脏. P.R.Halmos 6、只要一门科学分支能提出大量的问题, 它就充满着生命力, 而问题缺乏则预示着独立发展的终止或衰 亡. Hilbert 7、数学中的一些美丽定理具有这样的特性: 它们极易从事实中归纳出来, 但证明却隐藏的极深. 高斯 3、雷巴柯夫的常数与变数 俄国历史学家雷巴柯夫在利用时间方面是这样说的:“时间是个常数,但对勤奋者来说,是个‘变数’。用‘分’来计算时间的人比用‘小时’来计算时间的人时间多59倍。”
二、用符号写格言 4、华罗庚的减号 我国著名数学家华罗庚在谈到学习与探索时指出:“在学习中要敢于做减法,就是减去前人已经解决的部分,看看还有那些问题没有解决,需要我们去探索解决。” 5、爱迪生的加号 大发明家爱迪生在谈天才时用一个加号来描述,他说:“天才=1%的灵感+99%的血汗。”
6、季米特洛夫的正负号 著名的国际工人运动活动家季米特洛夫在评价一天的工作时说:“要利用时间,思考一下一天之中做了些什么,是‘正号’还是‘负号’,倘若是‘+’,则进步;倘若是‘-’,就得吸取教训,采取措施。” 三、用公式写的格言 7、爱因斯坦的公式 近代最伟大的科学家爱因斯坦在谈成功的秘诀时,写下一个公式:A=x+y+z。
并解释道:A代表成功,x代表艰苦的劳动,y代表正确的方法,Z代表少说空话。” “如果用小圆代表你们学到的知识,用大圆代表我学到的知识,那么大圆的面积是多一点,但两圆之外的空白都是我们的无知面。
圆越大其圆周接触的无知面就越多。”-芝诺 柯西(A. L. Cauchy, 1789 – 1857) Men pass away, but their deeds abide. 人总是要死,但是,他们的业绩永存。
拉普拉斯(Laplace, 1749 – 1827) What we know is not much. What we do not know is immense. 我们知道的是很少的,我们不知道的是无限的。 埃尔米特(C. Hermice 1822 – 1901) Abel has left mathematicians enough to keep them busy for 500 years. 他评价阿贝尔(Abel)时,曾经说:「阿贝尔留下的可以使数学家忙碌五百年。
」 普尔森(Poisson, Siméon 1781-1840) "Life is good for only two things, discovering mathematics and teaching 。
3. 小学一到五年级数学知识重点汇总(详细)
小学五年级全科目课件教案习题汇总语文数学三 单 元 有两个相对的面是正方形,长方体中相对的面完全相同;有12条棱,相对的棱长度相等;有8个顶点。
2、正方体的特征:正方体有6个面,这6个面都是正方形,所有的面完全相同;有12条棱,所有的棱长度相等;有8个顶点。 正方体可以看成是长、宽、高都相等的长方体。
3、相交于一个顶点的3条棱的长度分别叫做长方体的长、宽、高。 4、长方体或者正方体的12条棱的总长度叫做他们的棱长总和。
长方体的棱长总和=(长+宽+高)*4, 用字母可以表示为=C?长方体(a+b+h)4。 正方体的棱长总和=棱长*12,用字母可以表示为=12aC正方体。
5、长方体或者正方体6个面的总面积叫做它的表面积。 长方体的表面积=(长*宽+长*高+宽*高)*2,用字母表示为=(ab+ah+bh)2S?长方体。
正方体的表面积=棱长*棱长*6,用字母表示为2=6aS正方体。 6、物体所占空间的大小叫做物体的体积。
计量体积要用体积单位,常用的体积单元有立方厘米、立方分米、立方米,用字母表示为3cm、3dm、3m。3311000dmcm?,3311000mdm?。
7、棱长是1 cm的正方体,体积是13cm。一个手指尖的体积大约是13cm。
棱长是1 dm的正方体,体积是13dm。一个粉笔盒的体积大约是13cm。
棱长是1 m的正方体,体积是13m。用3根1 m长的木条,做成一个互成直角的架子架在墙角,它的体积是13cm。
8、长方体的体积=长*宽*高,用字母表示为=abhV长方体。 正方体的体积=棱长*棱长*棱长,用字母表示为3=aV正方体。
长方体和正方体的统一公式:支柱体的体积=底面积*高。 9、容器所能容纳物体的体积,叫做它的容积。
计量容积一般就用体积单位,计量液体的体积,常用容积单位升和毫升,用字母表示是L和ml。 4 311Ldm?,311mlcm?,11000Lml? 10、长方体或正方体容器的容积的计算方法,跟体积的计算方法相同。
但是要从容器里面量出长、宽、高。 11、形状不规则的物体,求他们的体积,可以用排水法。
水面上升或者下降的那部分水的体积就是物体的体积。 第 四 单 元 一、分数的意义 1、在进行测量、分物或计算时,往往不能正好得到整数的结果,这时常用分数来表示。
2、一个物体、一些物体等都可以看做一个整体,把这个整体平均分成若干份,这样的一份或几份都可以用分数来表示。把什么平均分,什么就是单位“1”。
3、把单位“1”平均分成若干份,表示其中的一份的数叫做分数单位。一个分数的分母越大,分数单位越小;一个分数的分母越小,分数单位越大。
4、分数与除法的关系:分数可以表示整数除法的商;除法里的被除数相当于分数中的分子,除数相当于分数里的分母,出号相当于分数线。 =?被除数被除数除数除数,=?分子分子分母分母。
5、求一个数是另一个数的几分之几的解题方法:用除法计算。 =?一个数一个数另一个数另一个数在解决问题中,要先找出单位“1”和比较量,一般来说,问题中“是”或“占”的后面是单位“1”,前面的比较量,如果没出现这两个字,要根据题意判断, 再根据公式“1=1?比较量比较量单位“”单位“” ”计算。
6、低级单位化高级单位(用分数表示)时,等于低级单位的数值两个单位间的进率,能约分的要约成最简分数。 二、真分数和假分数 1、分子比分母小的分数叫做真分数,真分数小于1; 分子比分母大或者分子和分母相等的分数叫做假分数,假分数大于1或等于1; 由整数部分(不包括0)和真分数合成的分数叫做带分数。
2、假分数化成整数或带分数,要用分子除以分母。当分子是分母的倍数时,5 能化成整数;当分子不是分母的倍数时,能化成带分数,商是带分数的整数部分,余数是分数部分的分子,分母不变。
3、带分数化成假分数,用原来的分母做分母,用分母和整数的乘积再加上原来的分子作分子,用式子表示成:+=?分母整数分子带分数分母三、分数的基本性质、约分、通分 1、分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。可以利用分数的基本性质,对分数进行约分或通分,或者把分母化成指定的分母或分子的分数。
2、两个数公有的因数,叫做它们的公因数。其中最大的公因数叫做它们的最大公因数。
当两个数成倍数关系时,较小的数就是他们的最大公因数;当两个数只有公因数1时,它们的最大公因数就是1.(公因数只有1的两个数叫做互质数) 3、求两个数的最大公因数,可以用列举法分别列出这两个数的因数,再寻找公有的因数。也可以用短除法计算。
4、分子和分母只有公因数1的分数叫做最简分数。 把一个分数化成和它相等,但分子分母都比较小的分数叫做约分。
约分时可以用分子和分母的公因数(1除外)去除,一步步来约分,也可以直接用最大公因数去除,直接约分。 5、两个数公有的倍数叫做它们的公倍数,其中最小的倍数叫做它们的最小公倍数。
一般情况下,求一个数的倍数可以用列举法、图示法、大数翻倍法、短除法。当两个数是倍数关系时,大数就是它们的最小公倍数;互质的两个数的最小公倍数是它们的积。
6、把异分母分数分别化成和原来的分数相等的同。
4. 小学一至五年级数学概念知识点梳理
基本公式: 1 每份数*份数=总数 总数÷每份数=份数 总数÷份数=每份数 2 1倍数*倍数=几倍数 几倍数÷1倍数=倍数 几倍数÷倍数=1倍数 3 速度*时间=路程 路程÷速度=时间 路程÷时间=速度 4 单价*数量=总价 总价÷单价=数量 总价÷数量=单价 5 工作效率*工作时间=工作总量 工作总量÷工作效率=工作时间 工作总量÷工作时间=工作效率 6 加数+加数=和 和-一个加数=另一个加数 7 被减数-减数=差 被减数-差=减数 差+减数=被减数 8 因数*因数=积 积÷一个因数=另一个因数 9 被除数÷除数=商 被除数÷商=除数 商*除数=被除数 小学数学图形计算公式: 1 正方形 C周长 S面积 a边长 周长=边长*4 C=4a 面积=边长*边长 S=a*a 2 正方体 V:体积 a:棱长 表面积=棱长*棱长*6 S表=a*a*6 体积=棱长*棱长*棱长 V=a*a*a 3 长方形 C周长 S面积 a边长 周长=(长+宽)*2 C=2(a+b) 面积=长*宽 S=ab 4 长方体 V:体积 s:面积 a:长 b: 宽 h:高 (1)表面积=(长*宽+长*高+宽*高)*2 S=2(ab+ah+bh) (2)体积=长*宽*高 V=abh 5 三角形 s面积 a底 h高 面积=底*高÷2 s=ah÷2 三角形高=面积 *2÷底 三角形底=面积 *2÷高 6 平行四边形 s面积 a底 h高 面积=底*高 s=ah 7 梯形 s面积 a上底 b下底 h高 面积=(上底+下底)*高÷2 s=(a+b)* h÷2 8 圆形 S面积 C周长 π d=直径 r=半径 (1)周长=直径*π=2*π*半径 C=πd=2πr (2)面积=半径*半径*n 9 圆柱体 v:体积 h:高 s;底面积 r:底面半径 c:底面周长 (1)侧面积=底面周长*高 (2)表面积=侧面积+底面积*2 (3)体积=底面积*高 (4)体积=侧面积÷2*半径 10 圆锥体 v:体积 h:高 s;底面积 r:底面半径 体积=底面积*高÷3 和差问题的公式: 总数÷总份数=平均数 (和+差)÷2=大数 (和-差)÷2=小数 和倍问题 和÷(倍数-1)=小数 小数*倍数=大数 (或者 和-小数=大数) 差倍问题 差÷(倍数-1)=小数 小数*倍数=大数 (或 小数+差=大数) 植树问题 1 非封闭线路上的植树问题主要可分为以下三种情形: ⑴如果在非封闭线路的两端都要植树,那么: 株数=段数+1=全长÷株距-1 全长=株距*(株数-1) 株距=全长÷(株数-1) ⑵如果在非封闭线路的一端要植树,另一端不要植树,那么: 株数=段数=全长÷株距 全长=株距*株数 株距=全长÷株数 ⑶如果在非封闭线路的两端都不要植树,那么: 株数=段数-1=全长÷株距-1 全长=株距*(株数+1) 株距=全长÷(株数+1) 2 封闭线路上的植树问题的数量关系如下 株数=段数=全长÷株距 全长=株距*株数 株距=全长÷株数 盈亏问题 (盈+亏)÷两次分配量之差=参加分配的份数 (大盈-小盈)÷两次分配量之差=参加分配的份数 (大亏-小亏)÷两次分配量之差=参加分配的份数 相遇问题 相遇路程=速度和*相遇时间 相遇时间=相遇路程÷速度和 速度和=相遇路程÷相遇时间 追及问题 追及距离=速度差*追及时间 追及时间=追及距离÷速度差 速度差=追及距离÷追及时间 流水问题 顺流速度=静水速度+水流速度 逆流速度=静水速度-水流速度 静水速度=(顺流速度+逆流速度)÷2 水流速度=(顺流速度-逆流速度)÷2 浓度问题 溶质的重量+溶剂的重量=溶液的重量 溶质的重量÷溶液的重量*100%=浓度 溶液的重量*浓度=溶质的重量 溶质的重量÷浓度=溶液的重量 利润与折扣问题 利润=售出价-成本 利润率=利润÷成本*100%=(售出价÷成本-1)*100% 涨跌金额=本金*涨跌百分比 折扣=实际售价÷原售价*100%(折扣利息=本金*利率*时间 税后利息=本金*利率*时间*(1-20%) 棱长总和:长方体棱长和=(长+宽+高)正方体棱长和=棱长*12熟记下列正反比例关系: 正比例关系:正方形的周长与边长成正比例关系长方形的周长与(长+宽)成正比例关系圆的周长与直径成正比例关系圆的周长与半径成正比例关系圆的面积与半径的平方成正比例关系 常用数量关系:1.路程=速度*时间 速度=路程÷时间 时间=路程÷速度工作总量=工作效率*工作时间 工作效率=工作总量÷工作时间 工作时间=工作总量÷工作效率总价=单价*数量 单价=总价÷数量 数量=总价÷单价总产量=单产量*面积 单产量=总产量÷面积 面积=总产量÷单产量 单位换算:长度单位:一公里=1千米=1000米 1米=10分米 1分米=10厘米 1厘米=10毫米 面积单位:1平方千米=100公顷 1公顷=100公亩 1公亩=100平方米 1平方千米=1000000平方米 1公顷=10000平方米 1平方米=100平方分米 1平方分米=100平方厘米 1平方厘米=100平方毫米体积单位:1立方千米=1000000000立方米 1立方米=1000立方分米 1立方分米=1000立方厘米1立方厘米=1000立方毫米 1立方分米=1升 1立方厘米=1毫升 1升=1000毫升 重量单位:1吨=1000千克 1千克=1000克时间单位:一世纪=100年 一年=四季度 一年=12月 一年=365天(平年) 一年=366天(闰年) 一季度=3个月 一个月= 3旬(上、中、下) 一个月=30天(小月) 一个月=31天(大月)一星期=7天 一天=24小时 一小时=60分 一分=60秒一年中的大月:一月、三月、五月、七月、八月、十月、十二月(七个月)一年中的小月:四月、六月、九月、十一月(四个月) 特殊分数值:=0.5=50% = 0.25 = 25% = 0.75 = 75% = 0.2 = 20% = 0.4 = 40% = 0.6 = 60% = 。
北师大版小学五年级数学上册知识点
第一单元《小数乘法》知识点
一、小数乘整数(利用因数的变化引起积的变化规律来计算小数乘法) 知识点一: 1、计算小数加法先把小数点对齐,再把相同数位上的数相加 2、计算小数乘法末尾对齐,按整数乘法法则进行计算。 知识点二: 积中小数末尾有0的乘法。先计算出小数乘整数的乘积后,积的小数末尾出现0,要再根据小数的性质去掉小数末尾的0。如:3.60“0”应划去 知识点三: 如果乘得的积的小数位数不够要在前面用0补足,再点上小数点。如0.02×2=0.04 知识点四: 计算整数因数末尾有0的小数乘法时,要把整数数位中不是0的最右侧数字与小数的末尾对齐。 思考: 小数乘整数与整数乘整数有什么不同? 1、小数乘整数中有一个因数是小数,所以积一般来说也是小数。 2小数乘法中积的小暑部分末尾如有0可以根据小数的基本性质去掉小数末尾的0而整数乘法中是不能去掉的。 二、小数乘小数 知识点一: 因数与积的小数位数的关系:因数中共有几位小数,积中就有几位小数。 知识点二: 小数乘法的一般计算方法: 先按整数乘法算出积,再给积点上小数点(看因数中一共有几位小数,就从积的右边起输出几位,点上小数点。)乘得的积的小数位数不够要在积的前面用0补足,在点小数点。 知识点三: 小数乘法的验算方法 1、把因数的位置交换相乘 2、用计算器来验算 三、积的近似数 知识点一: 先算出积,然后看要保留数位的下一位,再按四舍五入法求出结果,用约等号表示。 知识点二: 如果求得的近似数所求数位的数字是9而后一位数字又大于5需要进1,这是就要依次进一用0占位。如6.597保留两位为6.60 四、连乘、乘加、乘减 知识点一: 小数乘法要按照从左到右的顺序计算 知识点二: 小数的乘加运算与整数的乘加运算顺序相同。先乘法,后加法 整数乘法的交换律、结合律和分配律,对于小数乘法也适用。 五、简便运算 整数乘法的交换律、结合律和分配律,对于小数乘法也适用 计算连乘法时可应用乘法交换律、结合律将几位整数的两个数先乘,再乘另一个数,计算一步乘法时,可将接近整十、整百的数拆成整十整百的数和一位数相加减的算式,再应用乘法分配律简算。 对于不符合运算定律的算式,有些通过变形也可以应用。 乘法分配律也可以推广到相应的减法。 第二单元《小数除法》知识点 1、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。如:2.6÷1.3表示已知两个因数的积2.6与其中的一个因数1.3,求另一个因数的运算。 小数除法的计算方法: 计算除数是整数的小数除法,按整数除法的计算方法去除,商的小数点要和被除数的小数点对齐,整数部分不够除,商0,点上小数点,继续除;如果有余数,要添0再除。 计算除数是小数的除法,先把除数转化成整数,除数的小数点向右移动几位,被除数的小数点也要向右移动几位,位数不够时,在被除数的末尾用0补足,然后按照除数是整数的小数除法进行计算。 2、取近似数的方法: 取近似数的方法有三种,①四舍五入法②进一法③去尾法 一般情况下,按要求取近似数时用四舍五入法,进一法、去尾法在解决实际问题的时候选择应用。 取商的近似数时,保留到哪一位,一定要除到那一位的下一位,然后用四舍五入的方法取近似数。没有要求时,除不尽的一般保留两位小数。 3、循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。依次不断重复出现的数字,叫做这个循环小数的的循环节。 4、循环小数的表示方法: 一种是用省略号表示,要写出两个完整的循环节,后面标上省略号。如:0.3636……1.587587…… 另一种是简写的方法:即只写出一组循环节,然后在循环节的第一个数字和最后一个数上面点上圆点。如:12. 5、有限小数:小数部分的位数是有限的小数,叫做有限小数。 6、无限小数:小数部分的位数是无限的小数,叫做无限小数。 第三单元《观察物体》知识点 1、从不同的角度观察物体,看到的形状可能是不同的;观察长方体或正方体时,从固定位置最多能看到三个面。 2、正面、侧面、后面都是相对的,它是随着观察角度的变化而变化。通过观察、想象、猜测,培养空间想象力和思维能力,能正确辨认从正面、侧面、上面观察到的简单物体的形状。 3、构建空间想象力: (1)、将两个完全一样的正方体并排放,要求想象画出以不同角度看到的样子(强调左右面是重合,故只能看见一个正方形)。 (2)、将一个正方体和圆柱体并排放,要求想象画出从不同角度看到的样子。 4、动手操作,思维拓展 用5个小正方体摆从正面看到的图形(你能摆出几种不同的方法)。(有多少种不同摆法,最少要用多少个小正方体,最多只能用多少个小正方体。)北师大版小学数学五年级(上册)知识点
第一单元 小数除法
1、除数是整数的小数除法计算法则:除数是整数的小数除法,按照整数除法的法则去除,商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数,就在余数后面添0再继续除。
2、除数是小数的小数除法计算法则:除数是小数的除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数末尾用0补足),然后按照除数是整数的小数除法进行计算。
3、连除的算式可以写成被除数除以几个数的积,但除以几个数的积时,必须给这个相乘的式子加上小括号。
4、在小数除法中的发现:
①当除数不为0时,除数大于1时,商小于被除数。如:3.5÷5=0.7
②当除数不为0时,除数小于1时,商大于被除数。如:3.5÷0.5=7
5、小数除法的验算方法:
①商×除数=被除数(通用) ②被除数÷商=除数
6、商的近似数:根据要求要保留的小数位数,决定商要除出几位小数,再根据“四舍五入”法保留一定的小数位数,求出商的近似数。例如:要求保留一位小数的,商除到第二位小数可停下来;要求保留两位小数的,商除到第三位小数停下来……如此类推。
7、循环小数:
A、小数部分的位数是有限的小数,叫做有限小数。如,0.37、1.4135等。
B、小数部分的位数是无限的小数,叫做无限小数。如5.3… 7.145145…等。
C、一个数的小数部分,从某位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。(如5.3… 3.12323… 5.7171…)
D、一个循环小数的小数部分,依次不断重复的数字,叫做小数的循环节。(如5.333… 的循环节是3, 4.6767…的循环节是67, 6.9258258…的循环节是258)
E、用简便方法写循环小数的方法:
①只写一个循环节,并在这个循环节的首位和末位上面记一个小圆点
②例如:只有一个数字循环节的,就在这个数字上面记一个小圆点,5.333…写作5.3 ;有两位小数循环的,就在这两位数字上面,记上小圆点,7.4343…写作7.4 3 ;有三位或以上小数循环的,在首位和末位记上小数点,10.732732…写作10.732
8、除法中的变化规律: ①商不变性质:被除数和除数同时扩大或缩小相同的倍数( 0除外),商不变。②除数不变,被除数扩大,商随着扩大。 ③被除数不变,除数缩小,商扩大。
9、小数的四则混合运算顺序与整数四则混合运算的运算顺序相同。
第二单元 轴对称和平移
轴对称:
1.轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,那条直线就叫做对称轴。两图形重合时互相重合的点叫做对应点,也叫对称点。
2.轴对称图形的性质:对应点到对称轴的距离相等,对应点连线垂直于对称轴。
3.轴对称图形具有对称性。
4.轴对称图形的法:
(1)找出所给图形的关键点,如图形的顶点、相交点、端点等;
(2)数出或量出图形关键点到对称轴的距离;
(3)在对称轴的另一侧找出关键点的对称点;
(4)按照所给图形的顺序连接各点,就画出所给图形的轴对称图形。
平移:
1.平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
2.平移的基本性质:
(1)平移不改变图形的形状和大小,只改变图形的位置。
(2)经过平移,对应线段,对应角分别相等;对应点所连的线段平行且相等。
3.平移图形的画法:
(1)确定平移的方向与距离。
(2)将关键点按所需方向平移所需距离。
(3)按原来图形的连接方式依次连接各对应点。
4、平移几格并不是指原图形和平移后的新图形之间的空格数,而是指原图形的关键点平移的格数。
设计图案的基本方法:平移、对称
1.运用平移设计图案的方法:
(1)选好基本图案;
(2)根据所选的基本图案确定平移的格数和方向;
(3)平移,描出对应点;
(4)按顺序连接对应点
2.运用对称设计图案的方法:
(1)先选好基本图案;
(2)依据基本图案的特点定好对称轴;
(3)选好关键点,并描出关键点的对应点;
(4)按顺序连接对应点,画出基本图形的对称图形
第三单元 倍数和因数
像0,1,2,3,4,5,6,…这样的数是自然数。
像-3,-2,-1,0,1,2,3,…这样的数是整数。
我们只在自然数(零除外)范围内研究倍数和因数。
倍数与因数是相互依存的关系,要说清谁是谁的倍数,谁是谁的因数。
补充知识点:一个数的倍数的个数是无限的,因数个数是有限的。
一个数最小的因数是1,的因数是它本身;一个数最小的倍数是它本身,没有的倍数。
(一)2,5的倍数的特征
2的倍数的特征: 个位上是0,2,4,6,8的数是2的倍数。
5的倍数的特征: 个位上是0或5的数是5的倍数。
偶数和奇数的定义: 是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
补充知识点:
既是2的倍数,又是5的倍数的特征:个位上是0的数既是2的倍数,又是5的倍数。(既是2的倍数,又是5的倍数都是整十数,最小的两位数是10,最小的三位数是100)
(二)3的倍数的特征
一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。
同时是2和3的倍数的特征: 个位上的数是0,2,4,6,8,并且各个数位上的数字的和是3的倍数的数,既是2的倍数,又是3的倍数。(同时是2和3的倍数,一定是6的倍数,最小的是6。)
同时是3和5的倍数的特征: 个位上的数是0或5,并且各个数位上的数字的和是3的倍数的数,既是3的倍数,又是5的倍数。(同时是3和5的倍数,一定是15的倍数,最小的是15。)
同时是2,3和5的倍数的特征: 个位上的数是0,并且各个数位上的数字的和是3的倍数的数,既是2和5的倍数,又是3的倍数。(同时是2,3和5的倍数,一定是30的倍数,最小的两位数是30,最小的三位数是120)
9的倍数的特征:一个数各个数位上的数字的和是9的倍数,这个数就是9的倍数,它也一定是3的倍数。
四找因数
在1~100的自然数中,找出某个自然数的所有因数。方法:1、运用乘法算式,思考:哪两个数相乘等于这个自然数,那么这两个乘数就是这个数的因数。2、运用除法算式,思考这个数除以几能整除,那么除数和商就是这个数的因数。
补充知识点:
一个数的因数的个数是有限的。其中最小的因数是1,的因数是它本身。找一个数的因数,通常用列举的方法,可一对一对的写出来,也可按从小到大的顺序来写。
五找质数
一个数只有1和它本身两个因数,这个数叫作质数。
一个数除了1和它本身以外还有别的因数,这个数叫作合数。
1既不是质数也不是合数。
判断一个数是质数还是合数的方法:
一般来说,首先可以用“2,5,3的倍数的特征”判断这个数是否有因数2,5,3;如果还无法判断,则可以用7,11等比较小的质数去试除,看有没有因数7,11等。只要找到一个1和它本身以外的因数,就能肯定这个数是合数。如果除了1和它本身找不到其他因数,这个数就是质数。
六数的奇偶性
运用“列表”“画示意图”等方法发现规律:
小船最初在南岸,从南岸驶向北岸,再从北岸驶回南岸,不断往返。通过“列表”“画示意图”的方法会发现“奇数次在北岸,偶数次在南岸”的规律。
通过计算发现奇数、偶数相加奇偶性变化的规律:
偶数+偶数=偶数 奇数+奇数=偶数 偶数+奇数=奇数
偶数-偶数=偶数 奇数-奇数=偶数 偶数-奇数=奇数
奇数-偶数=奇数
偶数×偶数=偶数 偶数×奇数=偶数 奇数×奇数=奇数
第四单元 多边形面积
一比较图形的面积
借助方格纸,能直接判断图形面积的大小。
平面图形面积大小的比较有多种方法:
根据图形面积的大小,可以直接进行比较;可以借助参照物进行比较;可以运用重叠的方法进行比较;借助方格,利用数方格的的方法进行比较;直接计算面积后再进行比较等。
图形面积相同,其形状可以是不同的。
补充知识点:
确定一个图形面积的大小,不仅是根据图形的形状,更重要的是根据图形所占格子的多少来确定。
二地毯上的图形面积
知识点:
根据地毯上所给图案探求不规则图案面积的计算方法。
直接通过数方格的方法,得出答案的面积。
将图案进行“化整为零”式的计算,即根据图案的特点,将整体的图案分割为若干个相同面积的小图案,通过求小图案的面积,得出整个图案的面积。
采用“大面积减小面积”的方法,即通过计算相关图形的面积,得到所求的面积。
补充知识点:
在解决问题时,策略和方法是多种多样的。
三动手做
认识平行四边形、三角形与梯形的底和高。
从平行四边形一边的某一点到对边画垂直线段,这条垂直线段就是平行四边形的高,这条对边是平行四边形的底。
三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
从梯形的两条平行线中的一条上的某一点到对边画垂直线段,这条垂直线段就是梯形的高,这条对边就是梯形的底。
高和底的关系是对应的。
用三角板画出平行四边形的高的方法:
把三角板的一条直角边与平行四边形的一条边重合,让三角板的另一条直角边过对边的某一点。从这一点沿着三角板的另一条直角边向它的对边画垂线,这条垂线(从点到垂足)就是平行四边形一条边上的高。
注意:从一条边上的任意一点可以向它的对边画高,也可以从另一条边上的任意一点向它的对边画高。
用三角板画出三角形的高的方法:
把三角板的一条直角边对准三角形的一个顶点,另一条直角边与这个顶点的对边重合。从这个顶点沿着三角板的另一条直角边向它的对边画垂线,这条垂线(从顶点到垂足)就是三角形形一条边上的高。
用三角板画梯形的高的方法:
用同样的方法,画出梯形两条平行线之间的垂直线段,就是梯形的高。
(一)平行四边形的面积
平行四边形的面积=拼成的长方形的面积
长方形的长就是平行四边形的底;长方形的宽就是平行四边形的高。
因此:平行四边形面积=底×高
如果用S表示平行四边形的面积,用a和h分别表示平行四边形的底和高,那么,平行四边形的面积公式可以写成:S=a h
补充知识点:
当平行四边形的底和高相同时,其面积也是相同的。
(二)三角形的面积
三角形面积=两个相同三角形拼成的平行四边形的面积÷2
三角形的底和高,也就是平行四边形的底和高。
因此:三角形面积=平行四边形的面积÷2=底×高÷2
如果用S表示三角形的面积,用a和h分别表示三角形的底和高,那么,三角形的面积公式可以写成:S=a h÷2
补充知识点:
决定三角形面积的大小的因素不是图形的形状,而是三角形的底与高的长度,只要底和高相同,不同形状的三角形的面积也是相同的。
(三)梯形的面积
梯形面积=两个相同梯形拼成的平行四边形的面积÷2
梯形的上底与下底的和就是平行四边形的底,梯形的高就是平行四边形的高。
因此:梯形面积=平行四边形面积÷2=底×高÷2=(上底+下底)×高÷2
如果用S表示梯形的面积,用a和b分别表示梯形的上底和下底,用h表示梯形的高,那么,梯形的面积公式可以写成:S= (a+b)h÷2
补充知识点:
决定梯形面积的大小的因素不是图形的形状,而是梯形的上、下底之和与高的长度,只要上下底的和与高相同,不同形状的梯形的面积也是相同的。
等底等高的三角形的面积相等。
等底等高的平行四边形的面积相等。
第五单元 分数的意义
一分数的再认识
整体“1”的含义:一个物体或一些物体都可以看作一个整体,这个整体可以用自然数“1”来表示,通常叫做整体“1”。
分数的意义:把整体“1”平均分成若干份,其中的一份或几份,可以用分数表示。分母是几,整体就被分成了几份,分子是几,就表示其中的几份。
分数对应的“整体”不同,分数所表示的部分的大小或具体数量也不一样,即分数具有相对性。同一个分数对应的整体大,表示的具体数量就大;对应的整体小,表示的具体数量就小。同一个分数表示的具体数量大,对应的整体就大;表示的具体数量小,对应的整体就小。
二(真分数与假分数)
理解真分数、假分数、带分数的意义。
像 、 、 、 ,…这样的分数叫作真分数。特点:分子都比分母小;分数值小于1。
像 、 、 、 ,…这样的分数叫作假分数。特点:分子比分母大,或者分子与分母相等;分数值大于或等于1。
像 ,这样的分数叫作带分数。特点:由整数和真分数两部分组成的;分数值大于1。
带分数的读法: 读作:二又四分之一。
补充知识点:
分子是分母倍数的假分数可以化成整数; 分子不是分母倍数的假分数可以化成带分数。
三分数与除法
理解分数与除法的关系:被除数÷除数= (除数不为0)。
分数的分母不能是0。因为在除法中,0不能做除数,因此根据分数与除法的关系,分数中的分母相当于除法中的除数,所以分母也不能是0。可以用分数来表示两数相除的商。分数的分子相当于除法中的被除数,分母相当于除数,分数线相当于除号,分数的值相当于商。
根据分数与除法的关系把假分数化成带分数的方法:用分子除以分母,把所得的商写在带分数的整数位置上,余数写在分数部分的分子上,仍用原来的分母作分母。
把带分数化成假分数的方法:将整数与分母相乘的积加上原来的分子作分子,分母不变。
四分数基本性质
分数的分子和分母都乘上或除以相同的数(0除外),分数的大小不变。
分子相当于被除数,分母相当于除数,被除数和除数同时乘或除以相同的数(0除外),商不变。因此分数的分子和分母都乘或除以相同的数(0除外),分数的大小也是不变的。
求一个数是另一个数的几分之几:一个数÷另一个数= ,即比较量÷标准量= ,得到的商表示两个数的关系,没有单位名称。
五找公因数
几个数公有的因数是这几个数的公因数,其中的一个是它们的公因数。
找两个数的公因数和公因数的方法:
列举法:运用找因数的方法先分别找到两个数各自的因数,再找出两个数的因数中相同的因数,这些数就是两个数的公因数;再看看公因数中的是几,这个数就是两个数的公因数。
补充知识点:
其他找公因数的方法:
找两个数的公因数和公因数,可以先找出两个数中较小的数的因数,再看看这些因数中有哪些也是较大的数的因数,那么这些数就是这两个数的公因数。其中的就是这两个数的公因数。
例如:找15和50的公因数和公因数:
可以先找出15的因数:1,3,5,15。再判断4个数中,哪几个也是50的因数,只有1和5,1和5就是15和50的公因数。5就是它们的公因数。
3、如果两个数是不同的质数,那么这两个数的公因数只有1。
4、如果两个数是连续的自然数(0除外),那么这两个数的公因数只有1。
5、如果两个数具有倍数关系,那么较小的数就是这两个数的公因数。
六约分
把一个分数的分子、分母同时除以公因数,分数的值不变,这个过程叫做约分。
理解最简分数的含义:
像 这样分子、分母公因数只有1了,不能再约分了,这样的分数是最简分数。 分子与分母是相邻的自然数的分数一定是最简分数;分子分母是两个不同质数的分数一定是最简分数;分子是“1”的分数一定是最简分数。
掌握约分的方法:
约分的方法一般有两种,一种是用两个数的公因数一个一个去除,另一种是直接用两个数的公因数去除。
补充知识点:
比较分数大小时,分母相同的、分子相同的可以直接比较,有些时候分子分母都不相同可以采用约分后进行比较的方法。例如: ○
七找最小公倍数
两个数公有的倍数叫做这两个数的公倍数,其中最小的一个,叫做最小公倍数。
找两个数的公倍数和最小公倍数的方法:
1、先找出两个数各自的倍数(限制一定的范围内),再找出公有的倍数,找出两个数公有的倍数,看看这些公倍数中最小的是几,这个数就是两个数的最小公倍数。
两个数公倍数的个数是无限的,因此只有最小公倍数没有的公倍数。
补充知识点:
其他找公倍数和最小公倍数的方法:
2、找两个数的公倍数和最小公倍数,可以先找出两个数中较大的数的倍数(限制一定的范围内),再看看这些倍数中有哪些也是较小的数的倍数,那么这些数就是这两个数的公倍数。其中最小的就是这两个数的最小公倍数。
例如:找6和9的公倍数和最小公倍数。(50以内)可以先找出9的倍数(50以内)有:9,18,27,36,45,再从这些数中找出6的倍数18,36,18和36就是6和9的公倍数,18是最小公倍数。
3、如果两个数是不同的质数,那么这两个数的最小公倍数是两个数的乘积。
4、如果两个数是连续的自然数(0除外),那么这两个数的最小公倍数是两个数的乘积。
5、如果两个数具有倍数关系,那么较大的数就是这两个数的最小公倍数。
6、短除法求最小公倍数
八分数的大小
把分母不相同的分数化成和原来分数相等、并且分母相同的分数,这个过程叫作通分。
通分的两个要点:和原来分数相等;分母相同。
■分数大小比较:
同分母分数相比较,分子越大分数越大。 同分子分数相比较,分母越小分数越大。
分子分母都不相同的分数相比较的方法:
用通分的方法把分母不相同的分数化成和原来分数相等、并且分母相同的分数,再比较大小。(把两个分数化成分子相同的分数,再比较大小)
补充知识点:通分一般以最小公倍数作分母。
第六单元 组合图形的面积
组合图形面积
知识点:了解组合图形:有几个简单的图形拼出来的图形,我们把它们叫做组合图形。
计算组合图形的面积的方法是多种多样的。一般运用的方法是“分割法”和“添补法”。
分割法,即将这个图形分割成几个基本的图形。分割图形越简洁,其解题的方法也将越简单,同时又要考虑分割的图形与所给条件的关系。
添补法,即通过补上一个简单的图形,使整个图形变成一个大的规则图形。
探索活动:成长的脚印
知识点:能正确估计不规则图形面积的大小。
能用数格子的方法,计算不规则图形的面积。
估计、计算不规则图形面积的内容主要是以方格图作为背景进行估计与计算的,所以借助方格图能帮助建立估计与计算不规则图形面积的方法。
数方格的方法:满格记为1,少于半格记为0,大于半格记为1。
尝试与猜测
鸡兔同笼 知识点:运用列表的方法(逐一列表法、跳跃列表法、折中列表法)解决类似于“鸡兔同笼”的问题,也可用“方程”来解决。
点阵中的规律 知识点:能在观察活动中,发现点阵中隐含的规律,体会到图形与数的联系。在“点阵中的规律”的活动中,通过观察前后图形中点的变化规律,推理出后续图形中点的数量。
第七单元 可能性
1、判断游戏是否公平,要看事件发生的可能性是否相等。
2、摸球游戏(用分数表示可能性的大小)
(1)通过游戏所列的条件,推测某种情况出现的概率;
(2)能判断事件发生可能性的大小,写出所有可能发生的情况,推测可能发生的结果。
知识点:用分数表示可能性的大小。
客观事件中,“不可能”出现的现象用数据表示为“可能性是0”,客观事件中,“一定能”出现的现象用数据表示为“可能性是“1”,当可能性是相等的时候,用数据表述是“ ”。
逐步体会到数据表示的简洁性与客观性。
好了,今天关于“五年级上册数学知识点整理归纳”的话题就讲到这里了。希望大家能够对“五年级上册数学知识点整理归纳”有更深入的认识,并且从我的回答中得到一些帮助。









